martes, 27 de octubre de 2015
Sentido y dirección de un vector en R3
Representación geométrica y componentes de un vector.
Gráficamente, un vector se representa como una flecha ubicada en un eje de coordenadas. En esta flecha podemos identificar cada uno de los elementos que lo conforman y que estudiamos en el apartado anterior, además de algunos más.
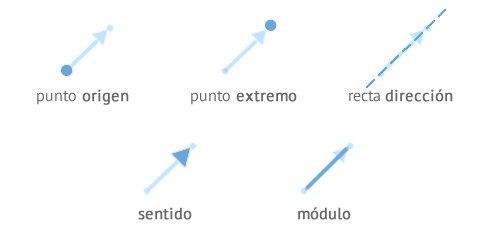
- Tienen un punto desde el que nace la flecha llamado origen o punto de aplicación.
- De igual forma, tienen otro punto donde termina la flecha llamado extremo.
- La recta sobre la que "descansan" los puntos de extremo y origen se denomina dirección o recta soporte.
- La distancia entre el punto origen y extremo corresponde con su módulo. A mayor distancia entre ellos, el módulo será mayor.
- La punta de la flecha determina su sentido, dentro de los dos posibles que se podría dibujar siguiendo su dirección, es decir hacia un lado de la recta o hacia el otro.
Sustracción de vectores
Sustracción de Vectores
Analíticamente
El vector es una magnitud que se grafica como un segmento que tiene su origen en un punto A y se orienta hacia su extremo (el punto B). El vector, por lo tanto, es un segmento AB.
La resta de vectores es una operación que se realiza con dos de estos segmentos. Para realizar la resta de dos vectores, lo que se hace es tomar un rector y sumarle su opuesto.
Supongamos que deseamos realizar la siguiente resta: AB – DE, siendo AB (-3, 4) y DE (5, -2)
(-3, 4) – (5, -2)
(-3-5, 4+2)
(-8, 6)
Como se puede apreciar, a -3 le sumamos el opuesto de 5 (es decir, -5), mientras que a 4 le sumamos el opuesto de -2 (o sea, 2). Así, el resultado de esta resta de vectores es (-8, 6).
Gráficamente
Método cola punta
Se traza el vector a, y en la punta de la flecha se traza el vector b, el resultado será el vector que sale de la cola del vector a y llega a la punta del vector b.
Método del paralelogramo
Este método se puede usar para restar solamente dos vectores, se trazan los vectores desde un mismo punto y se trazan líneas paralelas a cada vector para formar un paralelogramo, el resultado será el vector que va desde el origen hasta la esquina opuesta en diagonal.
Adición de vectores.
Suma analítica de vectores
Como vemos, un vector es un segmento orientado. Así pues, en el plano un vector no es más que un trozo de recta, en el que se diferencia claramente su origen y su extremo.
Vamos ahora a señalar qué son las componentes de un vector, antes de definir la suma analítica de vectores: son dos valores que vienen dados en forma de par de números, los cuáles indican las unidades que tenemos que desplazarnos horizontalmente y verticalmente para llegar desde el origen del vector al extremo de éste.
Es decir si el vector v = (3,2), esto nos indica que debemos desplazarnos tres unidades a la derecha y dos unidades hacia arriba para llegar del origen al extremo del vector.
Para sumar dos vectores analíticamente se suman sus respectivas componentes.
Suma de vectores por el método gráfico
Existen dos métodos para resolver una suma de vectores por el método gráfico:
Método cola a punta
En este método se utilizan la regla y el transportador, existen reglas generales y son las siguientes:
- Usar la misma escala para todos los vectores
- Trazar un vector (el orden no es importante)
- Trazar el segundo vector, empezando desde el final del primer vector (la punta de la flecha), hay que dibujar correctamente el vector cuidando el ángulo, longitud y sentido.
- La suma de los dos vectores es la flecha que se traza desde el principio del primer vector hasta la punta del segundo.
Ejemplo:
Tenemos los siguientes vectores:
La resultante a+b+c es el vector que une el inicio (cola) del vector “a” con la punta del vector “c”.
Método del paralelogramo
Para hacer una suma de vectores gráficamente por este método, se trazan los dos vectores desde el mismo origen y se forma un paralelogramo usando los vectores como lados adyacentes, el vector resultante es la diagonal que se traza desde el origen.
Ejemplo:
Tenemos los siguientes dos vectores:
Trazamos los dos vectores desde el mismo origen:
Suscribirse a:
Comentarios (Atom)


